Hypergraph is a generalization of the graph, wherein an edge can join any number of vertices. In contrast, in an ordinary graph, an edge connects exactly two vertices. It is often desirable to study hypergraphs where all hyperedges have the same cardinality; a $k$-uniform hypergraph is a hypergraph where all its hyperedges have size $k$. Hypergraph learning is a technique conducting learning on a hypergraph structure. Here, we provide an general introduction to Hypergraph Learning.
We will introduce the basic concepts of hypergraphs in the first place, then we will discuss several classic methods of hypergraph generation, and finally we will demonstrate four representative hypergraph learning examples from the shallower to the deeper.
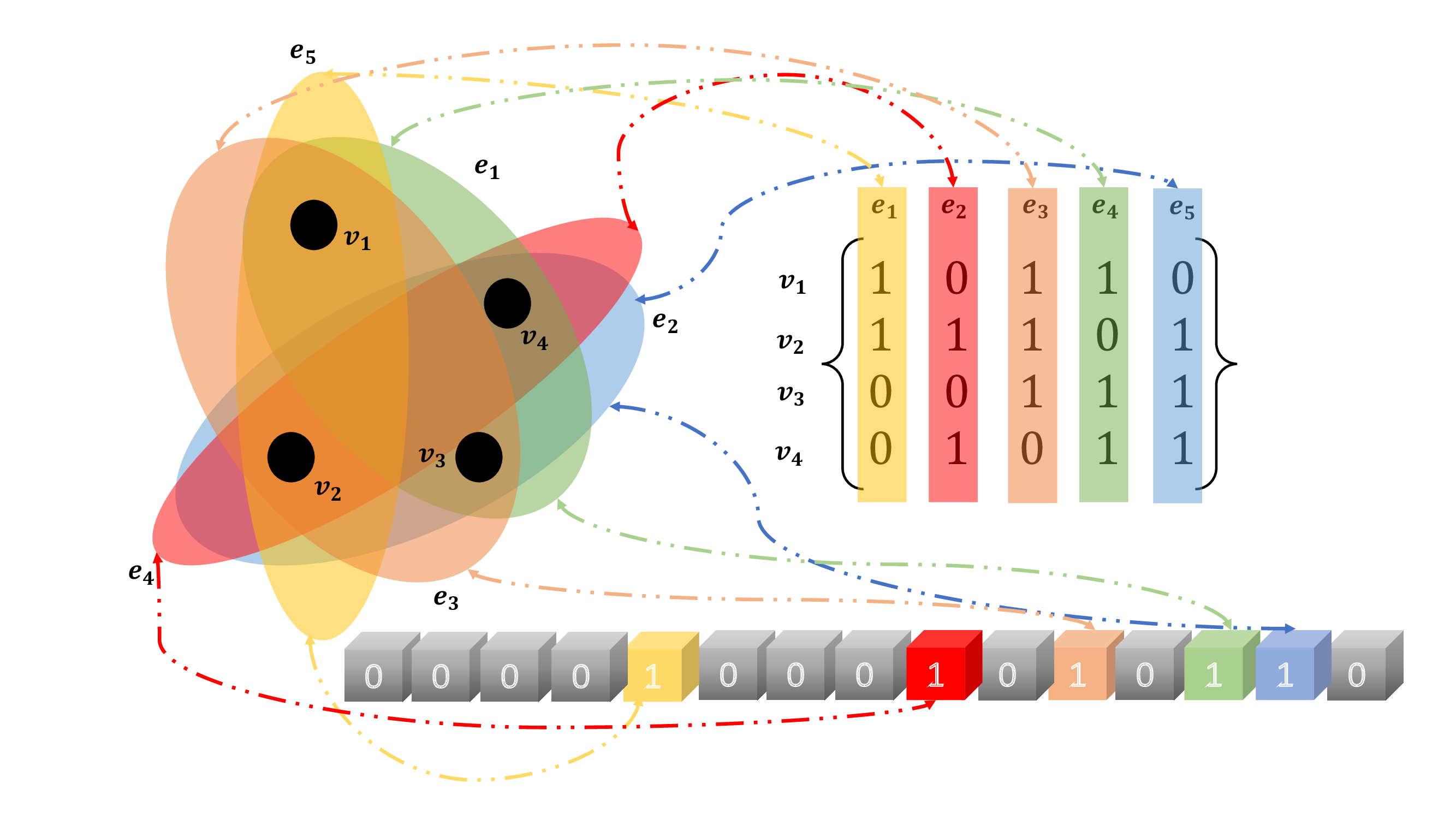
A hypergraph is a generalization of a graph in which an edge can join any number of vertices. In contrast, in an ordinary graph, an edge connects exactly two vertices. It is often desirable to study hypergraphs where all hyperedges have the same cardinality. For instance, a $k$-uniform hypergraph is a hypergraph such that all its hyperedges have the same size $k$. Noting that the size $k$ of a hyperedges means how many vertices are conneected by the hyperedge. Let's take the following example to understand it:
We take the demo of Hypergraph as an example to explain those components via illustrating them in the following table.
| $e_1$ | $e_2$ | $e_3$ | |
|---|---|---|---|
| $v_1$ | 1 | 1 | 0 |
| $v_2$ | 1 | 0 | 0 |
| $v_3$ | 0 | 1 | 1 |
| $v_4$ | 1 | 0 | 1 |
| $v_5$ | 0 | 1 | 1 |
| vertex | $v_1$ | $v_2$ | $v_3$ | $v_4$ | $v_5$ | hyperedge | $e_1$ | $e_2$ | $e_3$ |
|---|---|---|---|---|---|---|---|---|---|
| degree | 2 | 1 | 2 | 2 | 2 | degree | 3 | 3 | 3 |
Compared with graphs, hypergraphs have a stronger expressive ability and unique advantages for modeling more complex data. Hypergraphs are useful in modeling such things as satisfiability problems, databases, machine learning, and Steiner tree problems. They have been extensively used in machine learning tasks as the data model and classifier regularization. The applications include Recommendation System, image retrieval, and bioinformatics. Representative hypergraph learning techniques include hypergraph spectral clustering that extends the spectral graph theory with hypergraph Laplacian and hypergraph semi-supervised learning that introduces extra hypergraph structural cost to restrict the learning results. For large-scale hypergraphs, a distributed framework built upon Apache Spark is also available.
To capture the data correlation with a hypergraph, the first step is to construct a hypergraph from the data. The quality of the generated hypergraph structure directly affects the effectiveness of the data correlation modeling. The problem of how to construct an effective hypergraph is not trivial and thereby has been extensively investigated. Hypergraph generation can generally be divided into two categories: implicit and explicit.
The implicit hyperedges are defined as the hyperedges that are not able to be directly obtained from raw data and need to be reconstructed by establishing representations and measurements. Implicit methods can be further divided into distance-based and representation-based hypergraph generation methods. These methods can be applied to the tasks where we can create the representation of each subject and metrics to describe the similarity between samples.
Representation-based hypergraph generation methods formulate the relations among vertices through feature reconstruction.
Distance-based hypergraph generation approaches to exploit the relations among vertices using the distance in the feature space. The main objective is to find neighboring vertices in the feature space and construct a hyperedge to connect them. Specifically, there are two ways to construct this hyperedge: nearest-neighbor searching and clustering. In nearest-neighbor-based methods, hyperedge construction needs to find the nearest neighbors for each vertex. Different from nearest neighbor-based methods, the clustering-based methods aim to directly group all vertices into clusters by a clustering algorithm such as k-means and connect all vertices in the same cluster by a hyperedge. Noting that different scales of clustering results can be used to generate multiple hyperedges.
Let's take an exmaple of Distance-based Hypergraph Generation in the following to help understand hypergraph generation. We considered the examples where the feature space is a two-dimensional space and the distance is Euclidean distance, then several vertices closest to a center point form a hyperedge.
Explicit hyperedges can be established straightforwardly because the input data may inherently contain some structural information. Explicit methods can be further divided into attribute-based and network-based hypergraph generation methods.
Network data are available in many applications, such as social networks, reaction networks, cellular networks, and brain networks. For these data, the network data can be used to generate subject correlations.
Attribute-based hypergraph generation methods are those methods that employ the attribute information to construct a hyperedge. For example, the vertices sharing the same attributes are linked by a hyperedge. Hyperedge in an attribute-based hypergraph is regarded as a clique, and then the mean of the heat kernel weights of pairwise edges in this clique can be used as the hyperedge weight.
Let's take an example of Attribute-based Hypergraph Generation in the following to help understand hypergraph generation. We considered the examples where the basic information of several classmates is given, and each classmate acts as a vertex, then classmates with the same information can form a hyperedge.
| student | Chinese | Math | English | Physics | Chemistry |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | |
| 2 | 1 | 1 | 1 | ||
| 3 | 1 | 1 | 1 | ||
| 4 | 1 | 1 | |||
| 5 | 1 | 1 | 1 |
After a hypergraph is constructed, learning tasks, such as label prediction of unlabeled vertices, dynamic structure update, and multi-modal learning on this hypergraph, can be performed. In the following, we briefly introduce several representative hypergraph learning methods.
To apply hypergraph learning to a specific clustering task, there are three steps to do (Take the face recognition task as an example):
The figures above describes the process of how the hypergraph learning methods handle the clustering task.
MNIST is a picture dataset of handwritten digits for Classification. Here we'll use the MNIST dataset which consists of greyscale handwritten digits. Each image is 28x28 pixels, you can see a sample below.
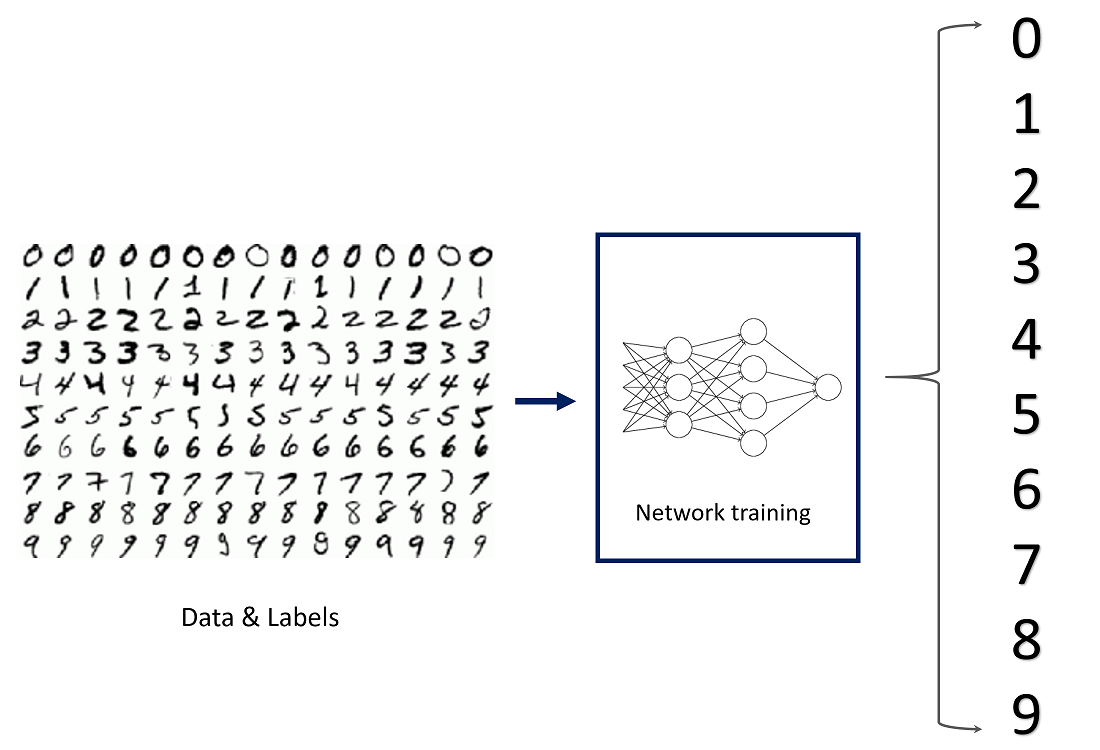
Our goal is to build a hypergraph that can take one of these images and predict the digit in the image. Let's get straight into it. Below is the full hypergraph we built, which contains all nodes in the test and training sets.
For better analysis, we extract the test set separately and show its corresponding hyperedge.
Experiments show that the hypergraph model can well represent the correlation information between various pictures and extract similar (common) features. Below are several representative hyperedges and the nodes they contain.
t-DHL leverage a tensor representation to characterize the dynamic hypergraph structure more flexibly. Unlike the incidence matrix, not only weights but the number and order of hyperedges can also be changed when optimizing the tensor representation. It is that the tensor representation can describe the hyperedges of all orders, which is a complete representation of hypergraph structure. The tensor-based dynamic hypergraph learning is formulated as a biconvex model to ensure that the model can converge to the optimal solution efficiently. T-DHL has the potential of applying to large-scale data due to its high effectiveness and low computational cost.
Microblog sentiment prediction is one of the common applications of hypergraph with wide application prospects. With the increasing proportion of multimodal tweets consisting of images, texts, and emoticons, new challenges have been raised to the existing sentiment prediction schemes. More crucially, it remains an open problem to model the dependency among multiple modalities, where one or more modalities may be missing. Therefore, a novel Bi-layer Multimodal Hypergraph learning (Bi-MHG) is put forward toward robust sentiment prediction of multimodal tweets to tackle the above challenges. In particular, Bi-MHG has a two-layer structure: The first layer, that is, a tweet-level hypergraph, learns the tweet-feature correlation and the tweet relevance to predict the sentiments of unlabeled tweets. The second layer, that is, a featurelevel hypergraph learns the relevance among different feature modalities (including the midlevel visual features in Sentibank) by leveraging prior multimodal sentiment dictionaries. These two layers are connected by sharing the relevance of multimodal features in a unified bilayer learning scheme. In such a way, Bi-MHG explicitly models the modality relevance rather than implicitly weighting multimodal features adopted in the existing Multimodal Hypergraph learning. Finally, a nested alternating optimization is further proposed for Bi-MHG parameter learning.
MHGNN is a multi-scale representation learning method on hypergraph for 3D shape
retrieval and recognition. Effective 3D shape retrieval and recognition are
challenging
but important tasks in computer vision research field, which have attracted much
attention in recent decades. Although recent progress has shown significant
improvement of deep learning methods on 3D shape retrieval and recognition
performance, it is still under investigated of how to jointly learn an optimal
representation of 3D shapes considering their relationships. In this method, the
correlation among 3D shapes is formulated in a hypergraph and a hypergraph
convolution process is conducted to learn the representations. Here, multiple
representations can be obtained through different convolution layers, leading to multi-scale representations
of 3D shapes. A
fusion module is then introduced to combine
these representations for 3D shape retrieval and recognition. MHGNN can investigat
the high-order correlation among 3D shapes, and the joint multi-scale representation
can be more robust for comparison.
Hypergraph Neural Network (HGNN) is currently the de-facto method for hypergraph representation learning. However, HGNN aims at single hypergraph learning and uses a pre-concatenation approach when confronting multi-modal datasets, which leads to sub-optimal exploitation of the inter-correlations of multi-modal hypergraphs. HGNN also suffers the over-smoothing issue, that is, its performance drops significantly when layers are stacked up. To resolve these issues, Residual enhanced Multi-Hypergraph Neural Network is put forward, which can not only fuse multi-modal information from each hypergraph effectively, but also circumvent the over-smoothing issue associated with HGNN.